Computer-Based Maths:
The Change
CBM is a new subject that starts from maths in the real world and works back to redefine the educational subject to match. A crucial change is to have computer-based (rather than human-powered) computation at its heart—redefining maths as the anchor subject for computational thinking across all subjects, centred on real-life problem solving, not historical hand-calculating techniques.
Computers liberated real-world maths from hand-calculating to go far further and faster than anyone could have imagined. Now it's vital that educational maths stands on this automation too.
The Problem
What's wrong with today's maths?
It's 80% a different subject from what is required in the real world. Computers have mechanised computation beyond previous imagination, yet today's maths education spends 80% of the curriculum time gaining expertise in hand–calculation methods rather than using a computer to do the calculating. The curriculum is ordered by the difficulty of the skills necessary to complete the calculation, rather than the difficulty of understanding the complexity of the topic. Computational difficulty rather than conceptual difficulty.
The very reason mathematics is seen as so important in education today is because mathematical or computational thinking skills appear so widespread and deeply embedded in all walks of life. But this is a relatively new phenomenon. Before mechanised computing, the use of mathematics above very basic arithmetic was much narrower and only applicable to fields such as some areas of physics and accountancy. It did not work well on anything requiring larger amounts of data, or messier or less immediately quantitative problems. Computers have made this fundamental change and without them many other current and rapidly emerging fields would not exist.
Traditional Method

CBM

The Fix
How will CBM fix the problem?
Fix 1The Right Basics
Students solve problems using the Computational Thinking Process (CTP). This is a process in which one creatively applies a four-step problem-solving cycle to real-world problems in order to develop and test solutions. The emphasis is learning how to take real-life situations and abstract them to a computational setting—often code—so that a computer can calculate the answer.
Some problems may require going through the cycle multiple times. It is helpful to represent this iteration as ascending a helix made up of a roadway of the four steps, repeating in sequence until “success” is declared.

-
Think through the scope and details of the problem, defining manageable questions to tackle. Identify the information you have or will need to obtain in order to solve the problem.
-
Transform the question into an abstract precise form, such as code, diagrams or algorithms ready for computation. Choose the concepts and tools to use to derive a solution.
-
Turn the abstract question into an abstract answer using the power of computation, usually with computers. Identify and resolve operational issues during the computation.
-
Take the abstract answer and interpret the results, recontextualising them in the scope of your original questions and sceptically verifying them. Take another turn to fix or refine.
Download the poster here for free.
Fix 2The right outcomes
Our curriculum follows an 11-category draft set of outcomes to reflect the needs of modern society (see the full set of outcomes here):
Thinking Outcomes
Step Outcomes
Our outcomes follow four core principles:
Outcomes should explicitly abstract out the thinking skills needed to tackle real-world problems using real-world technology. Skills like the ability to critique and verify a solution, or to generalise a model.
Outcomes come in varying levels of granularity. One outcome might be about the whole process; another might be about one step of it; another might be about just one small part within a step.
The Computational Thinking Process is iterative, multi-layered and complex. Outcomes should be broad, not limited to the concepts and tools of a specific problem.
If current assessment methodology cannot measure an outcome, that should not be a reason to remove it from the curriculum.
Fix 3A New Curriculum Based on Real-World Contexts
Our curriculum falls into five broad sectors (although these are by no means strict divisions):
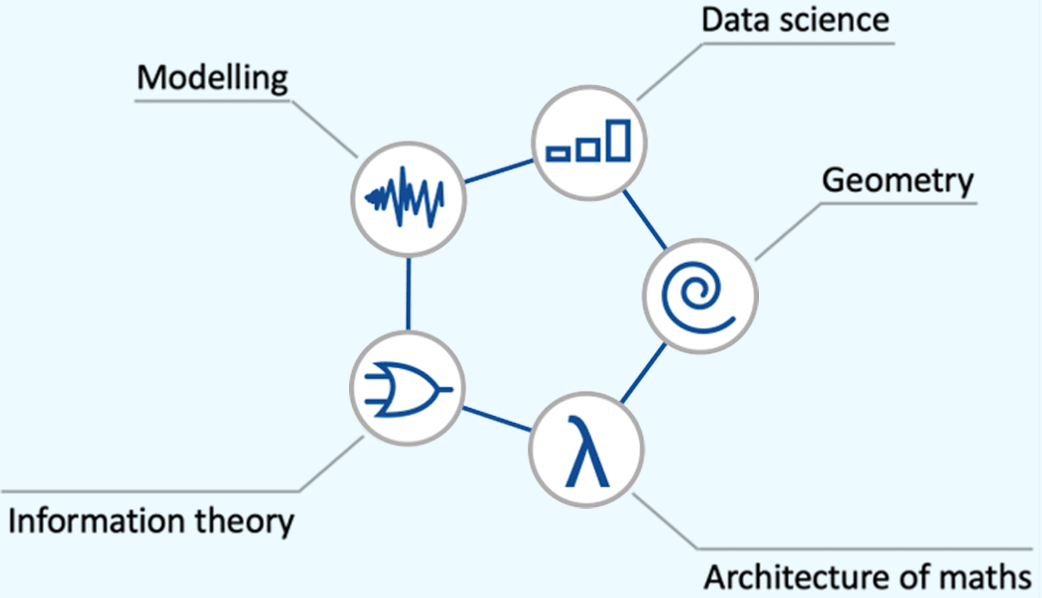
Traditional curricula are built upon outdated collections of mathematical concepts, making them poor representations of the problems people face in the world today.
We have taken the reverse approach: carefully choosing a selection of modern, real-world problems, then seeing how they map across mathematical concepts. By doing this, only concepts useful in the real world make the cut.
Fix 4Ready-to-Go Deliverables
Rather than separately specifying the curriculum and then building deliverables, building deliverables is part of our curriculum specification. Each deliverable, or module, is problem-centred, with students focusing on an overarching question that they can understand.
Modules can be delivered with the CBM Teacher Platform or as self-study versions, both leading learners through the Computational Thinking Process to solve a problem.
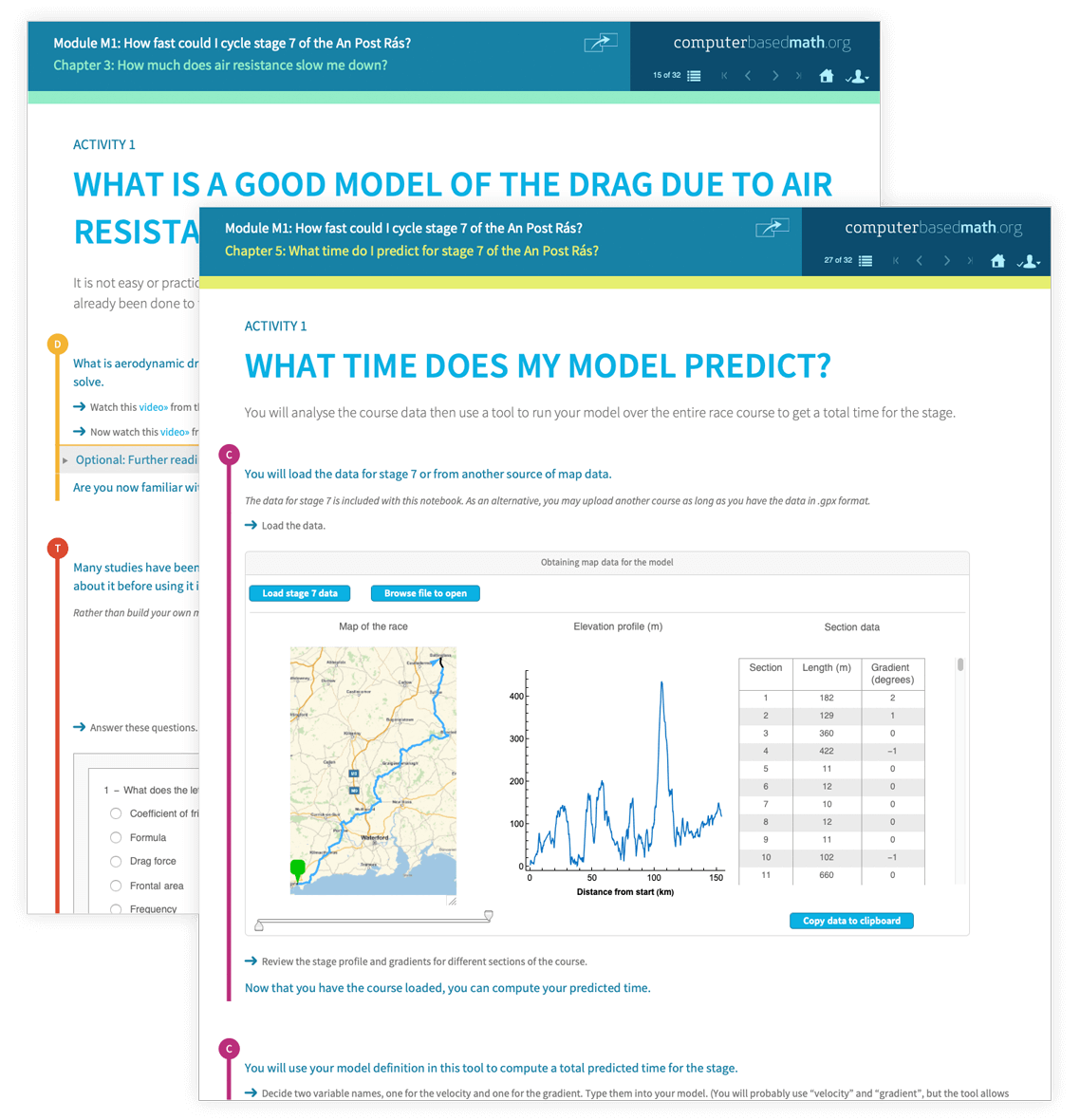
Within the compute step, students learn to drive the computer, so coding is integral to our approach. The Wolfram Language has the advantages of being easily understandable and having real-world knowledge built in.

At the end of each module, there is a final project where students independently transfer their skills and knowledge to another related context.

Each module comes with a certificate of completion and opportunities for assessment of the CBM outcomes.

The Fix: 1-Minute Summary
The Computational Thinking Room
Using the metaphor of a computational thinking room, we can put the fixes together: the four-step process, outcomes (across the whole process and within the process), concept learning stages, toolsets, categorisation areas and contexts. Different rooms may be customised to represent different contexts and the appropriate thinking, computation and outcomes that best apply.
Start the Change
What can I do now?
Read
The groundbreaking book that exposes why maths education is in crisis worldwide and how the only fix is a fundamentally new mainstream subject.
Buy nowCampaign for change
Do you agree with our five main principles for core computational curriculum change (MFC5)?
Find out moreRole by role: Action for you
Whether you are a student, policymaker, parent or educator, you'll find a list of ideas to get you started on the change to modern computational thinking.
Get started