Video: TED Global 2010 Talk
Transcript: Wolfram Technology Conference 2010 Talk
Conrad Wolfram | October 2010
Download CDF | PDF
I wanted to talk today about math education and then specifically reforming math education in a rather dramatic fashion, so if you've got eggs to throw, this is the time to prepare them!
I think we've got a real problem with math education, particularly in schools right now. Basically, no one's very happy. Most of those trying to learn it think it's boring and irrelevant. Employers think that people don't know enough. Governments realize it's critical for economic development, but don't know what to do about fixing it, and many teachers are frustrated, too. And yet, without question, math is more important to the world than it ever has been in human history. So at one end we've got falling interest in education in math and at the other, a world that's ever more quantitative, ever more mathematical than it has been. So what's gone wrong and how do we bridge this chasm? Well, actually I think the answer's really very simple: use computers. I want to talk through and explain why I think computers really are the silver bullet to making math education work but used dramatically.
To understand what I'm talking about, let's remind ourselves what math looks like in the real world. It's got lots of modeling, lots of simulation. It's not just for mathematicians, but for a huge range of other subjects: medical imaging, electrical engineering, etc. That's an important thing to understand, of course. And it's actually very popular. Now, look at math in much of education. It looks very different—lots of calculating, usually by hand or sometimes with a calculator and dumbed down problems.
Why teach math?
So to understand why this is, why these things have got so separated, why a chasm has opened up, let's first ask the question, why do we teach math? What is math? What do we mean by it? Well, I think there are sort of three reasons why we teach people math, in particular, why we teach it to everyone. Firstly there's technical jobs. Secondly what I call everyday living. Just being able to survive in a civilized society and prosper in it nowadays requires much more mathematical understanding than it ever did. And thirdly, what one might call logical mind training—being able to reason, whether with math itself or with other things. Math has given society a tremendous ability to go through logical reason.
What is math?
So the next question we might ask: what is math? And by that I mean what do we mean when we say we're teaching math or doing math? I reckon there are about four pieces to doing math: posing the right question. This is the one that is critically messed up in the outside world most of the time. You ask the wrong question and unsurprisingly, you tend to get the wrong answer. Then there's this step of taking that real world—it might be real, real world, it might be the theoretical world—and moving it to a kind of math formulation, turning it into the mathematical form that has been so useful. Then there's what I call step 3, which we'll come back to, actually computing—taking that formulation and turning it into the answer in a math formulation, manipulating it to the point where you get the result. And then there's, so to speak, transforming it back (step 4) from that mathematical form to real world and crucially verifying it. You might call that 4b.

Here's the funny thing. We insist that the entire population learns how to do step 3 by hand. Perhaps 80% of doing math education at school is step 3 by hand and largely not doing steps 1, 2, and 4. And yet step 3 is the step that computers can do vastly better than any human at this point, so it's kind of bizarre that that's the way around we're doing things. Instead, I think we should be using computers to do step 3 and we should be using students to do steps 1, 2, and 4 to a much greater extent than we are.
Calculating is the machine of math
The crucial point here is math is not equal to calculating. It's a much bigger subject. Now for a long time in the past, these two have been completely intertwined. Up until computers came, the limiting step in doing most math was the calculating step and there was no other way to do it. But now that's not the case. Math has been liberated from calculating. See, I think of calculating as the machinery of math, it's the mechanism for doing it. But it isn't an end in itself. It's a means to an end and I think it's really important to stand on the automation we now have with computers to go further.
And the critical thing to understand, this is no small problem. My calculation is that on an average school day in the world, we use up about 106 average lifetimes in students learning hand calculating around the world. So this is a pretty massive human endeavor. Worse, it's not even fun for most of them! They weren't even a fun 106 lifetimes!
Now I don't think all teaching of hand calculating is wrong. But I think we've got to be very specific about when it's needed; we should assume computers are the basis for all calculating and only when there's a real case for doing it by hand should we. Here's an example of such a case: I estimate things in my head quite often. I still think that's a useful thing to be able to do, but we don't really train people for that very much.
And the other crucial thing I want to make clear, I don't think that if somebody gets interested in hand calculating that that's a bad thing at all. That's a good thing. I kind of got interested in ancient Greek and that's great. If somebody gets excited about doing something, learning something, however bizarre it might seem or "un-useful," that's great. We should encourage them to do that. And of course, modern computers allow them to do that. But I wouldn't force the majority of people to learn ancient Greek. I wouldn't make it a compulsory subject in schools. And similarly, I wouldn't make what I would call the "history of hand calculating," our current math curriculum, compulsory either. But yet, we've got this fantastic subject that's really important in the world—let's call it Computer-Based Math™—that we do need everyone to learn, and that's what we need to focus on.
Get the basics first
So what are the reasons why people object to doing everything based on computer? Well, I thought I would pick out just a few, and these are the top three, I guess, I'm going to talk through what I tend to get asked.
Firstly they say, "You've got to get the basics first. You can't do anything without getting the basics first." By which they presumably imply learning by hand before using a computer. So, I ask, "Well, what do you mean by basics? Basics of what exactly?" Are the basics of driving a car learning how to service it? Or engineer it, for that matter? I don't think so. Are the basics of learning to write sharpening a quill? I don't think so either.
What we've crucially got to do is to separate what we're trying to get done from how it gets done. Now early on for cars, a hundred years ago, it was true that the mechanics of a car were pretty closely associated with driving it. There was no automation between, so you kind of had to be a mechanic to drive a car. But that's long since changed, and now the subject of driving is totally different than the subject of car mechanics. They got completely separated.
What we need to do is get people experience in what they're actually trying to do.
If you want to go drive a car, it's good to get experience in driving a car. That's different from experience in maintaining the car. It's automation that allows this separation between if you like the mechanics of how stuff is getting done and what you're trying to do in operating it. And cars have got lots of automation now; in fact they have better automation than any human could manage in any area—like how they set their fuel mixture. Well, increasingly computers put great automation levels between the mechanics of math, the calculating, and what you're trying to get done, too. When the automation gets good, you can go much further by doing it on the machine with a computer than you can by hand, and the subject of the mechanics of calculating becomes a distinct subject from using, applying, or doing math.
Another common mistake on this topic is mixing up the basics of a subject with the order of invention. To illustrate, I usually tell this story. My daughter used to like to make paper laptops, so she called them. And as you can see, this one's even specially branded!

So I said to her one day, "When I was your age, I didn't make paper laptops. Why do you think that was?" And she thought carefully for a couple of seconds and said, "No paper?" The point being if you are five years old, the order of invention doesn't really matter. We should just give students the best tools to do the job.
"Computers dumb math down"
Here's another argument that I hear: that if you use computers, it dumbs math down. This one is really frustrating. Somehow the idea has come about that, intrinsic to the use of computers, everything turns into mindless button pushing, intellectually all dumbed down. But if you do stuff by hand, it's all very intellectual and brain training.
Do we really believe most students studying math right now think it's anything other than fairly mindless? Most of the time what they're actually doing is running through a bunch of calculating processes they don't understand for reasons they don't get. Mindless or not, at least those processes had real practical use 50–100 years ago—they were the only way of calculating. But now they don't; almost nobody actually uses them anymore outside education.
So let's be clear about one thing: the mindlessness base we're starting from with hand calculating math is pretty low right now. And, far from thinking computers will dumb math down, I actually think, correctly applied, they can do quite the opposite. I think computers are the greatest tool for conceptually understanding math. As I've said, they liberate you from calculating to think at a higher level.
But like all tools, they can be used completely mindlessly—for example making endless multimedia presentations. There was one I saw which aimed to use a computer to show people how to solve an equation by hand—all the steps you would take by hand. Now, maybe that's good if you're excited about learning that, but it seems to me that it's completely backward for mainstream math. Why are we getting humans to learn with a computer how to solve an equation by hand that the computer should be solving anyway for them? They should be setting up the problem that the computer then solves, and working with the result.
So what I'm arguing for is open-ended use of computers. Use a computer as an open-ended tool as much as possible where the students are trying much harder problems. And, of course, as we all know, with a computer you can take a simple problem like solve 5x2+2x+1=7 but you can make it harder, for example solve 5x4+2x+1=7. The principle of the problem is still the same. The mechanics of calculating are harder.
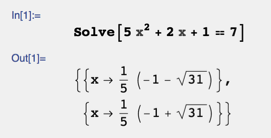

And if you really want to check that computers haven't dumbed down math, look in the outside world. Look in the real world. Do we honestly believe that science and engineering and all other things that depend on math have somehow got conceptually simpler since computers were introduced? Absolutely not. Computers have allowed them to drive far further forward, have allowed them to become much more conceptual because people can get rid of the calculating step and get the computers to do it.
So let's be quite clear where the problem is now. What's dumbed down is the complexity of current math problems; it's not that computers will dumb math down.
"Hand calculating procedures teach understanding"
So here's another objection, with which I have a bit more sympathy—that hand calculating procedures teach understanding. That by learning, let's say, how to solve an equation, you're somehow learning procedures that are themselves useful, or at least they train the idea of procedurizing things. That even if solving an equation itself is no longer useful to know how to do by hand, doesn't it teach logical thinking in some way that's somewhat useful?
Well, I think the answer is possibly yes. But I think there's a much better way to learn about procedures. It's called programming. That's how everybody specifies procedurizing things in the modern world. And it's also great because when you program stuff, particularly in a high-level language, you can check your understanding. You can't program unless you really understand the problem, and also the results you get are much more exciting. It's much more exciting to get a program to actually do interesting things than it is to go through five things you couldn't solve very well by hand when you can't remember the answer, whether you got to the right or wrong answer. So I think procedurizing learning, how that works, is important, but we have a great new way to do that.
More practical and more conceptual
A key point I'm making here is that we have an opportunity to reform math education so it's both more practical and more conceptual. We can simultaneously improve the vocational and the intellectual. Now, I think this is pretty unusual. I can't think of any other subject where one has had this opportunity. But because math itself as a subject has so fundamentally changed in the outside world with new computing technology, we have this opportunity in education.
If I wanted to pick the number one advantage of Computer-Based Math, I would say—massively accelerated experience and intuition. In the time you can do one hand calculation, you can do 20–30 calculations on the computer. They can be harder. They can have hair all over them. That's a really important part of it. You're not just always dealing with a simplified problem, the thing that was made especially for education. People can experience much more quickly. They can feel math in a way that they didn't before. It can be integral to their intuition, a natural way to experience the world. That's what we'd like to achieve.
Another key point, computers mean we can reorder the curriculum to be based on conceptual rather than computational complexity—as it is now. It's had to be that way around because you need to know how to do all computations by hand to delve into a particular topic. So an example I always pick: calculus. Why do we teach it so late? Why don't we teach calculus to 10-year-olds? Well, I think because it's been traditionally quite hard to compute. Doing integrals by hand is hard, but the concept of finding areas of things isn't particularly hard. There's no reason not to do it in a completely different order when computers do the calculating.
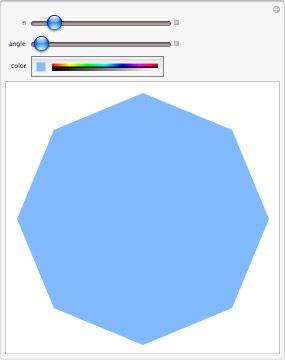
Here's a little example—very, very simple—but it gives a kind of intuition that one often doesn't get in normal school math.
So as you increase the number of sides, as you might expect, this turns into a circle. My daughter, then age four, could figure that out. And you could get into discussions of limits and that view of the world that people often don't get. (For this Demonstration, for this age group, it's also a very important feature of this demo that we are able to change the color).
There's no reason not to teach things like this early, and it's important that we do.
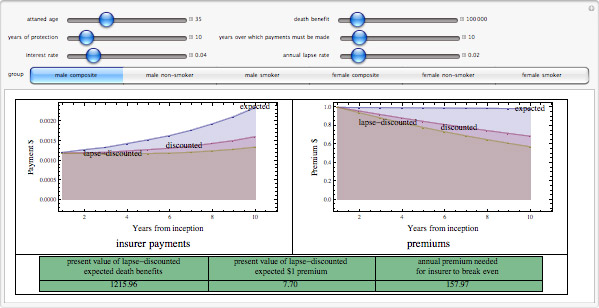
Another big blockage in reforming math education are exams. In the end, if we want the curriculum to get reformed, it's not any good if we then test them on how well they hand calculate in an exam. So we need computers in exams, and we want to be able to ask questions like this. This is one of Seth Chandler's Demonstrations, and it's real.
What's the best life insurance policy? This is a real thing that I want to try and optimize in difference cases. It's not just a toy example that we've made for some pure education reason. This is typical of a kind of question—how do I optimize some complicated model that's been set up—that just doesn't get asked right now and could be asked if we had computers in exams. Now, of course, by no means is this the only kind of question that needs to be asked, but it's one that people are very poorly optimized for right now.
Computer-Based Math: critical reform
So look, I believe Computer-Based Math is a critical reform and it's not an optional extra. It's also a reform that has much more importance and resonance with many more people than it did in the past; the technology is much better too and close to ubiquitous, but with all that it's certainly extremely difficult to pull off.
However difficult, it is vital. Let's recognize that it's a critical part of moving economies forward. I think it can take us from a knowledge economy to what I call a computational knowledge economy where high-level mathematical thinking is widespread—for many, not just the few—and those abilities rather than just base knowledge that one would term knowledge economies as having are driving the economy forward. The country to do this first will leapfrog others. And there's opportunity for developing as well as developed countries: their less developed math education infrastructure is easier to reform, faster.
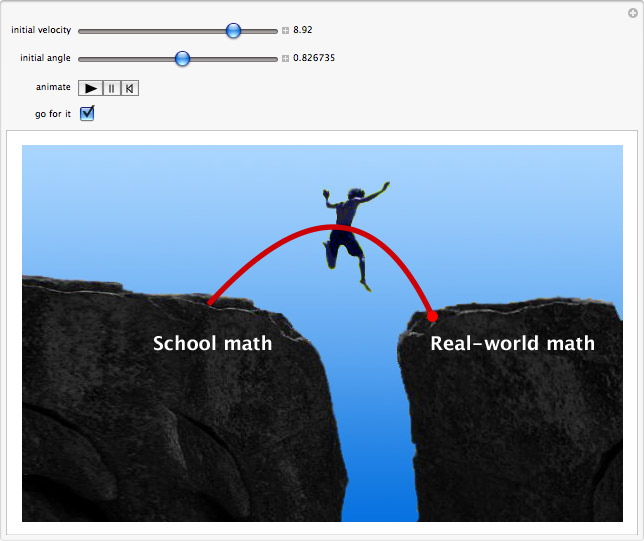
Let me be clear that I do not think this is an incremental kind of reform. Here's what happens if you walk rather slowly over a chasm is typically this. You go right into it. So what you need to do is start with a very high initial velocity (of course solving the differential equations correctly before you do) and jump over and hopefully get to the other side. Let's go for it!
Finally, I'm not even sure if the subject that one's talking about here is called math. Is the naming wrong? But whatever it's called, let's be quite clear: it's the mainstream subject of the future. Thanks.